比和比例的概念，在小學六年級的時候學生就已經學過了。而它的例子在日常生活中則隨處可見，如：看到一瓶酒，上面標示「酒精濃度百分之三十」，就可以知道這瓶酒裡頭，每一百公克的酒就有三十公克的酒精，也就是酒精和酒的比是30：100；或是在地圖上很常見的比例尺，如果標示1：10000就代表地圖上每一公分，就代表實際上的10000公分等。而在數學裡，比和比例亦是有著很廣泛的運用，如討論等比數列、等比級數或者是在幾何圖形中，在歐幾里得所寫的「幾何原本」這本數學史裡用過最久的教科書，比和比例也佔著一個很重要的地位。這裡來討論其中一種最為人所熟知的名詞--黃金分割。「黃金分割」這名詞在十九世紀後才出現，在之前則稱之為「中末比」。到底什麼是黃金分割呢？你可以在紙上畫出一線段AB，在線段AB上取一點C，如果AB：AC
= AC：CB，則稱C點把線段AB黃金分割，把C點稱為線段AB的黃金分割點；而稱比值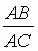
或
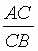為黃金分割數，以j 表示之。
而 j 的值究竟是多少？
因為
=
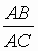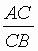= j
所以 AB = j AC，AC = j CB
把上面兩個式子代入 AB = AC + CB 後再將AC約去
可得 j = 1+
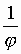
j 2 - j - 1= 0
因為j
是正數，所以可得到 j = 1+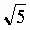
=1.648033...
以上黃金分割的資料請參閱趙文敏所編著的數論淺談或國立編譯館的國中數學教師手冊第二冊。