商高定理

名稱

        一般而言，西方國家都用「畢達哥拉斯定理」 (Pythagorean Theorem) 此名稱。在我國，有時簡稱其為「畢氏定理」，有時亦用「商高定理」、「勾股定理」「勾股弦定理」或「陳子定理」等名稱。這個定理名稱之所以如此多元化，實有其歷史的淵源。

       西方國家普遍相信「畢氏定理」是於西元前560年到西元前480年間由畢達哥拉斯發現的，或者至少是由他證明的。然而，近代數學史家對這個推論表示存疑（梁宗巨，民86b）。目前已有明確的證據顯示，畢達哥拉斯數（滿足a² + b² = c²之整數）的出現年代比畢達哥拉斯活著的年代早了一千多年。在1945年 Neugebauer 等人詮釋了一塊巴比倫泥板，發現巴比倫人在約西元前1900-1600年時已經知道至少15組畢達哥拉斯數。這塊泥板是由普林頓(G.A.Plimpton)收藏的第322號泥板，目前存放在哥倫比亞大學。雖然有許多證據顯示畢達哥拉斯並非此定理的創始者，然而因為早期許多哲學家、數學史家等推斷畢達哥拉斯發現了這個定理，故冠以「畢達哥拉斯定理」之名，許多人已經習慣了這個名稱，是以此名稱仍沿用至今。

到底畢達哥拉斯有沒有發現這個定理呢？因為畢氏曾到過巴比倫，有可能是由那兒學來的；而由畢氏欣喜若狂的情形來看，也有可能是他自己發現的，或是找到了證明的方法。所以，畢達哥拉斯是否發現此定理，目前並無定論（梁宗巨，民84b）

在我國，有關「商高定理」的記載，最早出現在《周髀算經》的趙君卿注中。卷上一開始就敘述了如下的一段：「昔者周公問於商高曰，竊聞乎大夫善數也，請問古者包犧立周天曆度，夫夫不可階而升，地不得尺寸而度，請問數安從出，商高曰數之法出於圓方，圓出於方，方出於矩，矩出於九九八十一，故折矩，以為句廣三，股脩四，徑隅五，既方之外半其一矩，環而共盤得三四五，兩矩共長二十有五是謂積矩，故禹之所以治天下者，此數之所生也，…」。由上述可知，商高（西周時大夫，約西元前1100年）已提到句（讀同勾）三、股四、弦五；且商高認為早在重治天下（治水）時即利用了這個性質。因為商高所提到的句三、股四、弦五是我國最早有關「商高定理」的記載，故有些人認為此定理應稱為「商高定理」。

然而商高所提到的是一個特別的直角三角形之邊長關係，即邊長為3、4、5的直角三角形其邊長的關係滿足3²+4²=5²，但是並無觸及一般性的「商高定理」。有關一般性「商高定理」的最早記載出現在《周髀算經》中對於陳子的敘述。在文中有一段如下的描述：「昔者榮方問於陳子，曰今者竊聞夫子之道，如日之高大，光之所照，一日所行，遠近之數，人所望見，四極之窮，列星之宿，若求邪至日者，以日下為句，高為股，句股各自乘，并而開方除之，得邪至日，從畢所旁至日所十萬里。」這段敘述除了指出三角測量的方法外，並提到「商高定理」的一般性原則「句股各自乘，并而開方除之」。因為這段敘述，所以有人認為此定理應稱為「陳子定理」。

也有一些人認為不知到底是由誰最先發現此定理，故不如避開人名，直接以「勾股弦定理」稱之，而有勾股必有弦，故亦稱為「勾股定理」。此名稱的由來，可追溯自《周髀算經》的趙君卿注。本頁引了《周髀算經》中的一段：「句廣三，股脩四，徑隅五」。在趙君卿這裡，「句廣三」中，「句」的注是：句亦廣；廣，短也。「股脩四」中，「股」的注是：股亦脩；脩，長也。放在此注中，句(同勾)代表短邊，股代表長邊。他同時指出句是橫放著的，而股是縱放著的，所以這時自然會形成一個直角。對於弦的用法則是從「徑隅五」的注而來，注中曰；徑，直；隅，角也；亦謂之弦。在趙君卿的注中，「徑」往往用來表示一線段的長，例如他用「圓徑一」表示圓的直徑是一，「方徑一」表示正方形的邊長為一。所以他所說的「徑隅五」是指橫放的勾和縱放的股形成的角(直角)所對應的直線段長度為五。而「徑隅」亦稱為弦，此乃「勾股弦定理」名稱的來源。從上面的說明有勾（橫放之短邊），股（縱放之長邊），則必有所對應之，故亦有人稱此定理為「勾股定理」。

內容

一般而言，對於「商高定理」有三種不同的表達方式（梁宗巨，民84a）

1. 直角三角形斜邊上的正方形等於直角達上的兩個正方形。

在此，「等於」意指「拼補相等」，所謂拼補相等指的是將直角邊上的兩個正方形經過刮分，再合併拼湊成斜邊上的正方形而言。此種說法，完全沒有從面積或數的觀點出發，而是只考慮圖形經過切割拼湊後的全等問題。為了區別於別種不同思維下的「商高定理」，也有學者專家稱此為「形的勾股定理」。

2. 直角三角形直角邊上的兩個正方形面積之和等於斜邊上正方形的面積。

雖然我們常用數量相等來表示面積相等的概念，但是，面積是幾何概念，且不一定要用數的計算才能判定面積的相等。所以，此種「商高定理」的概念可以說介於純粹的形及純粹的數之間。

3. 直角三角形斜邊長度的平方等於兩個直角邊長度平方之和。

這種「商高定理」強調長度的平方，並未涉及長度平方所代表的幾何意義。較強調單純的數的運算，故亦有人稱其為「數的勾股定理」。

證明

     「畢氏定理」的證明方法有許多種，目前已知有人收集到約370種之多（梁宗巨，民84a；曹亮吉，民85）。這些證明，有些可以看成很嚴密的證明；有些也可看成是「拼補相等」的證明。茲舉下列數例簡述之：

1. 幾何原本的證明（第一卷命題47）（梁宗巨，民84a；Euclid，1992 譯本）

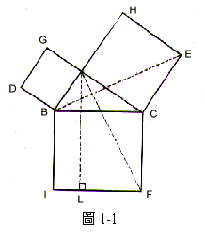
在直角三角形中，直角所對的邊上的正方形等於夾直角兩邊上正方形的和。歐幾里得的證法可簡述如下：如圖1-1

注:(1)歐幾里得是不區分全等與面積相等這兩個概念的。這兩種情形，他都用相等」來敘述(Euclid.1992)  。

    (2)在此譯本中，平行四邊形用兩個相對的頂點來代表；現在平行四邊形的記法都是用四個頂點來表示。

2. 趙爽（趙君卿）的證法（梁宗巨，民84a；錢寶琮，1981）：

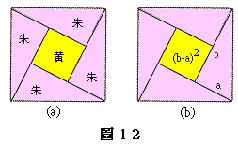
　　雖然在《周髀算經》中有陳子對一般性「商高定理」的描述；然而正式提出證明的應屬趙君卿。他在注中所提之「勾股圓方圖」的一部分，給出了「商高定理」的證明。其敘述如右：「勾股各自乘併之為弦實，開方除之即弦，案弦圖又可以勾股相乘為朱實二，倍之為朱實四，以勾股之差自相乘為中黃實，加差實，亦成弦實。」趙君卿一開始便點出了「商高定理」的一般性敘述：勾（短邊）、股（長邊）各自乘，自乘即平方，併之即“和起來”，為弦（斜邊）實，實即面積（或平方）。接下來他給出了一個證明，因為所附的圖已失傳，故後人根據所述證明，補繪了一圖如圖1-2(a)(錢寶琮，1981)：

　　依此圖(案弦圖)，將直角三角形互相垂直約兩邊相乘(以勾股相乘)，得到此朱色三角形面積約二倍(為朱實二)，此數的兩倍是朱色三角形面積的四倍(倍之為朱實四)，把(股一句)的平方當成中間黃色正方形的面積(以勾股之差自相乘為中黃實)，這個面積也稱為差實，把它加到剛才算出的朱色三角形面積的四倍上(加差實)，就得到直角三角形斜邊的平方(九成弦實)。這個證明以數學式子來說，即2ab + (b - a)² = c² （如圖1-2(b)）。

3. 畢氏學派的證法：

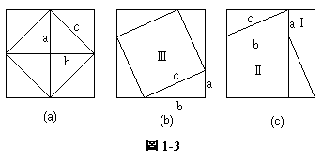
畢氏學派普研究鋪地磚的問題。他們由如圖1-3(a)這類等腰直角三角形的問題觀察出直角邊上的兩個正方形合起來正好是斜邊上的正力形。從此推出非等腰的情形。如圖1-3(b)，將以 a-b 為邊的正方形中之四個不直角三角形重新排至如圖1-3(c)中的位置，則可看出正方形III=正方形I + 正方形II ，得證。

4. Thabit ibn Qurra的證法：

Thabit ibn Qurra (約西元826-901)是阿拉伯數學家。他的方法是：對於任意給的直角三角形，以它的直角二邊為邊長的二正方形，可被切割後重新拼湊成以斜邊為邊長的正方形。

如圖1-4，任給直角三角形ABC，延長CB至D，使得CD=b，完成正方形ACDH；延長BD至E，使得DE=a，作 △BEF△ACB，完成正方形 GDEF；延長DH至I，使得GI=b；則△BEF移至△AHI，將ACB移至IGF即得證。

畢氏數(Pythagorean triple)

      畢氏數指的是滿足不定方程 x² + y² = z² 的正整數解。「畢氏定理」的代數表示法為

x² + y² = z²..…......(1)

       其中x與y表示直角三角形的二直角邊的長度，z表示斜邊的長度。通常我們把方程式(1)的正整數解(x，y，z)稱為「畢氏數」(或畢氏三元數、畢氏組數、勾股數)。

古埃及人及巴比倫人都提出了一些滿足(1)式的解。例如，約西元前2160-1700年時，埃及人即用試位法算出當 z² = 100時 x² + y² = z²的解為(6，8，10)。而巴比倫人也於約西元前1700年時，列出了15組畢氏數。故有些數學史家推論巴比倫人已掌握了一般的「畢氏定理」及畢氏數的公式（錢寶琮，1981）。

      畢達哥拉斯曾提出(1)式的一類解公式：(2n + 1，2n² + 2n，2n² + 2n + 1)。我們可以很容易的看出如(8，15，17)這組解就不是上面的形式，所以可知上面的型式不包含(1)式的所有解。柏拉圖（西元前421-前347）提出了另一類解公式：(2n，n² - 1，n² + 1)。同樣的，如（5，12，13）這組解就不是這種公式的型式。丟番圖提出了求出x² + y² = z²的有理數解之一般性方法。大約同時期，劉徽(梁宗巨，民84a)在《九章算術》第九章《勾股》中指出，其中m、n是互質的奇數。除此，他並作圖證明之。由此可見，劉徽已掌握了式(1)的一般解。直至七世紀初，(1)式的完整解答才由印度的婆羅摩岌多(Brahmagupta，西元598-665)於約西元628年，明確地給出。

現在我們就來看看畢氏數的全部解。因為若(x，y，z)為畢氏數，則，(kx，ky，kz)亦為畢氏數。因此不失一般性，可令欲求的畢氏數滿足(x，y，z) = 1。如此的畢氏數稱為(1)式的原解(或稱基本畢氏數、基本勾股數)。依此原則，有如下的定理：

定理：設x，y，z N且(x，y，z)= 1，若，x² + y² = z²，則存在互質且奇偶性

互異的自然數m、n，使得

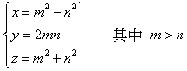
證明：欲證明，x、y必為一奇一偶。

         若x、y都是偶數，則x² + y² = z²必為偶數，此與

           (x，y，z)=1之假設不符。

         若x、y都是奇數，則可令

          z=2m+1，y=2n+1

         z²= x² + y² = (2m + 1) ² + (2+1) ²

　　　　　　　 = [4(m²+m)+1] + [4(n²+n)+1]

則z²=2(mod 4)，但偶數的平方與0同餘(模4)

奇數的平方與1同餘(模4)，不可能有數的平方與2同餘(模4)

故x、y不可能同為奇數。

由上可知了x，y必為一奇一偶。

不失一般性，設y為偶數，則x、z為奇數，

y² = z² - x² = (z - x)(z + x)..................?

欲證：(z - x，z + x)=2，

設(z - x，z + x)=d，則d|z-x且d|z+x，得d|2z且d|2x。

因為x，z為奇數了所以d|2，則d=1 or 2，

因為z-x，z+x，皆為偶數，所以d=2。

可令，z+x = 2u，z-x = 2v，其中(u,v)=1，

則，x=u-v，z=u+v，

因為y為偶數，所以可令y=2a，又由?式得

4a² = y² = (z+x)(z-x) = (2u)(2v) = 4uv ða² = uv，

因為(u，v)=1，所以u、v皆為完全平方數。

令u=m²，v=n²，則(m，n)=1，且

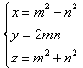
因為x為奇數，m及n必為一奇一偶。

注：上述係利用整數論的方法來證明。仍有代數、幾何等其他不同的證法(國立臺灣師範大學附屬中學，民81)。

多項式

代數的蓬勃發展引進了以文字符號代表的觀念(林炎金等，民72；趙文敏，民74)。文字符號的使用不斷演進，直至笛卡兒(Rene Descartes，1596~1650)時，才用英文字母中前面的幾個表示常數，後面的幾個表示未知數。

在早期，代數多半用來解決問題，所以一個文字符號的出現，所代表的往往是一個未知數。從丟番圖(Diophantus，三世紀)起，代數符號在方程式論中就扮演著重要的角色，而所代表的也都是未知數。直至十九世紀中葉，代數的發展跳出原有的束縛。向量、矩陣等的代數體系產生，使得代數體系的元素不再局限於數，且加與乘的運算也跳脫了數的範圍。近世抽象代數於是崛起。這種代數強調的是公設化。以公設的方法定義群、環、體、理想、模等等抽象數學概念。直至今日，代數的發展仍受到這種公設化的影響(趙文敏，民74)。

     在西元1882年以前，體的概念只局限於數系中，直至此年，考納克(Leopold Kronecker，1823~1891)突破了這個限制，引進了由若干未定元的所有有理式所成

的體，如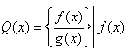，，且；，，且…。同時他還把所提的“把一個新數加上一個體，形成一個擴張體”(如把加到體Q上，形成一個Q的擴張體)的概念推廣到“把一個未定元加上一個體，形成一個擴張體”。(如把未定元x加到體Q上，形成一個Q的擴充體Q(x) )後來他發現，若α是一個超越數(如π、e等)，則將α加到有理數體Q上所得的擴充體Q(α)與以未定元x及Q所成的有理式體Q(x)是同構(趙文敏，民74；Stewart，1972)。於此，未定元x只是Q(x)這個體中的一個元素，並不一定是分析數學申所說的變數。

        對於多項式而言，因x為未定元，係數都是某一體F中之元素的多項式都可寫成的形式。為方便起見，我們常以?(x)、g(x)等表示之。要特別注意的是(零多項式)  a_i = 0 ，，1…，n。也就是說，像f(x)=3x-1，g(x)=2等這些多項式都不是零多項式。所以對於多項式與，f(x)=g(x) n=m且a₀=b₀，a₁=b₁，…，a_n=b_n ，因此Q[x]中多項式f(x)=3x-1與g(x)=2是不會相等的。同樣的，h(x)=2x² + x - 12與k(x)=2-3也是不相等的。

       在中學教材中，x 這個符號的使用往往在不同的時機時，代表了不同的意義。當我們在解一元一次方程式3x – 1 =2時，並非把3x - 1與2看成x的多項式，而是把它們視為未知數，只是這些未知數剛好以多項式的形式呈現，容易被人誤以為是多項式3x - 1與多項式2。

      如果x代表變動的數，那麼當x的值變動時，3x –1 、 2x² + x –12 、 2x-3等的值也隨著變動（2亦可看成是隨著x的值變動的特例），這時我們可以把x看成是自變數，3x –1 、 2x² + x –12 、 2x-3 、 2等看成是因變數，而自變數x與因變數之間的對應關係稱為函數關係。因為這類函數自變數與因變數的關係恰好以多項式的形式呈現，故我們亦稱其為多項式函數(就如、等分別稱為三角函數與指數函數的情形相同)。

        若多項式函數f(x)=3x-1(x視為變數)，則欲求X為何值時，f(x)的值為2(x視為未知數)，即相當於解一元一次方程式3x-1=2。同樣的，若h(x)=2x2+x-12及k(x)=2x-3為多項式函數時，欲求x為何值時，此二函數有相同的函數值，則相當於解一元二次方程2x2+x-12=2x-3。同樣的，當我們說求多項式函數h(x)= 2x2+x-12的根時，即是求自變數x的值是多少時能使得h的函數值(因變數)為0，此即相當於解一元二次方程式2x2+x-12=0，求出此方程式的根。

        由於上述因素，像2x2+x-12這類表示法中的x可視為未定元、變數、未知數等等。本尊與分身各有巧妙，不去細分。

此外，由於我們在作以x為未定元的多項式之加法與乘法運算時，為了便於表示其和與積，我們也將多項式f(x)與g(x)分別視為序列(ai)與(bi)，其中，，，。如此一來，，；，其中，。

除法演算法則 (Division Algorithm)

       一般而言，除法演算法則對於中學生，我們都用下面這樣的敘述：設f(x)、g(x)為二多項式且g(x)不為零多項式，則恰有唯一的二多項式q(x)及r(x)，使得f(x)=q(x)g(x)+r(x)其中r(x)=0或 deg r(x)<deg g(x)，上面的 f(x)=q(x)g(x)+r(x) 中，f(x)為被除式，g(x)為除式，r(x)為餘式。

　　事實上，這個演算法亦適用於 R 或 C 這類數系的情形。這點可從下面的比較看出：

　　令 R 是一個有單位元素的交換環。f(x)、g(x)是R[x]中二多項式，且g(x)的首項係數為可逆元，則恰有唯一的二個多項式q(x)及r(x)    R[x]，使得f(x)=q(x)g(x)+r(x)，其中r(x)=0 或 deg r(x)<deg g(x)。

餘式定理(Remainder Theorem)

       一般而言，對於中學生，我們都用下面這樣的敘述來說明餘式定理：多項式f(x)除以x-α的餘式等於f(α)。

       事實上，如同除法演算法則，這個定理也有較一般的敘述：令R是一個有單位元素的交換環。如果多項式f(x) R[x]且αR，則存在一個唯一的多項式q(x) R[x]，使得f(x)=(x-a)q(x)+f(α)。

指數與次數

指數

指數(Exponent)的名詞最早是由德國人施迪費爾(Michael Stifel，1487-1567)提出來的。在西元1484時，仍Chuquet提到像下面這樣兩行數列中，如果要算第二行任兩數的積，可將第一行中對應到它們的兩數相加，得到的數再對應回第二行的數即是積。

這個做法顯然已有兩平方數相乘即指數相加的觀念。施迪費爾在西元1544年把第一行數稱為Exponent (指數)。Exponent的原意是“代表人物”或“代表者”。施迪費爾可能是說要求兩數的積，只需求其“代表者”的和即可。爾後，此用語即成為正式的數學用語(梁宗巨，民84a)。

指數的概念經過了多次的擴展才有了現在的形式。早期指數一直代表同一數連乘的次數，所以只有可能是正整數。西元十四世紀時，奧雷姆(Nicole Oresme，約1323-1382，法國人)使用了指數為分數的概念；西元1655時，渥里斯（John Wallis，1616-1703，英國人）更進一步的使用了負指數的概念。西元1679年，萊布尼茲（Gottfried Wilhelm Leibniz，1646-1716，德國人）引入了變指數的觀念。至於虛指數則是於西元1719年由法尼亞諾（Giulio Carlo Fagnano dei Toschi，1682-1766，義大利人）所提出的。

指數的符號表示法經過多次的演變。例如，在1590牢時(王懷權，民81)，Vieta用N代表指數為1，Q代表指數為2，C代表指數為3，例如，7x記為7N，7x²記為7Q，7x³記為7C。1619時，Burgi用代表7、7^２、7³，。1631年，Harriot用7a、7aa、7aaa來表示。西元1634年，Herigone用7a、7a2、7a³表示。直至西元1637年，Descartes在其著作《幾何學》中，用7x、7xx、7x³表示才與目前的用法相同。然而在這本書中，Descartes有時亦用xx表示x²。雖然至此指數的符號用法已大致與現代相同，然而渥里斯在引入負指數時仍末使用Descartes的符號法則，宜至牛頓於西元1670年寫給萊布尼茲的信中方使用了與現在相同的分指數及負指數之符號。

次數

次數、次方、乘方之名稱在我國最早是以“冪”字出現。“冪”字在我國原意為覆蓋食物的巾或以巾覆蓋東西。引申為方形的東西、矩形的面積、兩數的積（或一數自乘的結果）。據載，《九章算術》申有一段敘述：「廣從步數相乘得積步。」在此廣指寬，從指長，長和寬的步數相乘得矩形的面積（以平方步表示）。劉徽在作其注中道：「此積謂田冪，凡廣從相乘謂之冪。」田指矩形，故此段的意思是：這裡所說的積是指矩形的面積，長和寬的乘積叫做冪。這是「冪」字第一次在數學的文獻中出現。爾後此字斷斷續續的出現在我國數學書中。直至我國數學漸與世界數學合流後，我們將Power翻譯為冪或乘方(梁宗巨，民84a)。近來也有將其譯為次方的說法。

二 、參考書目

[1] 王懷權 (民81)，數學發展史。臺北：學英文化事業有限公司。

[2] 李儼 (民81)，中國古代數學簡史。臺北：九章出版社。

[3] 林炎金等譯 (民72)，數學史─數學思想的發展。臺北：九章出版社。

[4] 國立編譯館 (民85)，國民中學數學教師手冊第三冊。臺北：國立編譯館。

[5] 國立編譯館 (民86)，國民中學數學課本第三冊。臺北：國立編譯館。

[6] 國立臺灣師範大學附屬中學 (民81)，高級中學數理叢書─數學充實教材（第一輯）教育部中等教育司。臺北：國立臺灣師範大學附屬中學。

[7] 梁宗巨 (民84a)，數學歷史典故。臺北：九章出版社。

[8] 梁宗巨 (民84b)，畢達哥拉斯，摘自世界名數學家傳記，第11-26頁文俊主編。北京：科學出版社。

[9] 曹亮吉 (民85)，阿草的葫蘆。臺北：遠哲科學教育基金會。

[10] 趙文敏 (民74)，數學史（第一卷）。臺北：協進圖書有限公司。

[11] 錢寶琮 (1981)，中國數學史。北京：科學出版社。

[12] Burton, D. (1971)，。臺北：協進圖書有限公司。

[13] Euclid. (1922), Elements, 藍紀正，朱恩寬譯，歐幾里得幾何原本。臺北：九章出版社。

[14] Eues, H. (1993), An introduction to the history of mathematics，歐陽絳譯，數學史概論。臺北：曉園出版社。

[15] Goldhaber, J. & Ehrlich, G. (1977), Algebra。臺北：協進圖書有限公司。

[16] Herstein, N. (1979), Topics in Algebra (2nd Ed.)。臺北：東南書報社。

[17] Stewart, L. (1972), Galois Theory。臺北：協進圖書有限公司。

[回前一頁]