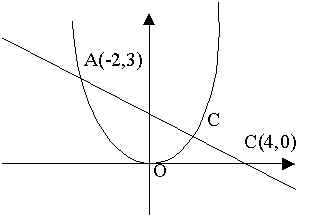
一對一
∴是函數
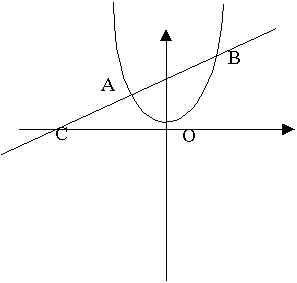
多對一
∴是函數
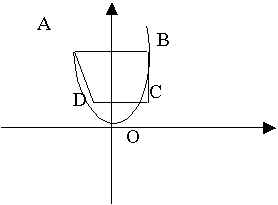
一對多
∴不是函數
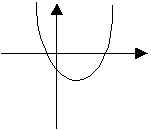
一對無
∴不是函數
4-1
變 數 與4-2 函 數
一輛汽車在高速公路上,以每小時90公里的速率行駛,行走x小時共走了y公里,那麼,y與x之間就有下列關係:y = 90 x 。
時間x ( 時 ) |
0 |
2 |
4 |
5 |
10 |
… |
里程y(公里) |
0 |
180 |
360 |
450 |
900 |
… |
當每一個x值確定時,y的值也隨著唯一確定。
函數:將兩個量的數值用符號x及y表示後,當x的值確定時,y的值也隨著唯一確定,亦即對於任意給定的一個x值,都恰有一個y值與它對應,這時我們說,y是x的函數。.
函數的判別法則:在x與y的對應關係中,若是“1對1
”或“多對1”,則為函數。若是“1對多”或“1對無”,則不為函數。
| (1)
一對一 ∴是函數 |
(2)
多對一 ∴是函數 |
(3)
一對多 ∴不是函數 |
(4)
一對無 ∴不是函數 |
練習:周長為30的長方形很多,若用x表示長方形的長,用y表示同一長方形的寬,
寫出x與y的關係式。y是不是x的函數?長分別是為1、2、3、4時,寬分別是多少?
自變數與應變數:對於y是x的函數,可以想像y值是著x值而改變的,我們把x叫做自變數,y叫做應變數。
例:右圖是一個簡單的電算器計算流程:
這個流程在輸入一個x值後,都恰好只有一個y值輸出,所以y是x的函數。若以文字f代表這個計算流程,那麼x經過f之後的結果可以寫成f(x),讀作“f of x”。由於y也代表輸出的數,因此y=f(x)。
函數的表示法:若
y是x的函數,可以寫成y=f(x)或y=g(x)、……等。例:上例中,「輸入
x」乘以5,再減7,變成「輸出y」,所以y=5x-7可記為f(x)=5x-7。函數值:
y=f(x)指當x值確定時,y的值也隨著唯一確定,y就是f (x)例如x=3時,y=f(3)亦即,與3對應的值就是f(3),f(3)叫做函數f在=三時的函數。例:若
f(x)=5 x-7,則f(x)=5×3-7=8也就是說對應於x=3的函數值是8。練習:設函數
f(x)=3(x-2)-5,分別求f在x=3、x=5及x=-4時的函數值。練習:一平年中x月有y天,用g表示這個函數,其關係可記為y=g(x)。
求:(1)g(1)=? (2)g(3)=?練習:一個農人想用籬笆圍成一個面積為
100平方公尺的長方形花圃,若長方 形的長為x公尺,寬為y公尺,x與y的關係式。寫出
若此函數用
f表示,寫出f(x)。當長為
10公尺時,寬是多少? [回前一頁]