1-1
簡易二次函數的圖形1.
前言﹕以前曾學過線型函數與二元一次方程式,其圖形坐標平面上是一直線,那麼二次函數的圖形又是如何?如何描繪它的圖形?它有什麼特性?這是本節所要討論的重點。2.
二次函數的意義:若一函數等是右邊為一個x的二次多項式,這樣的函數叫做二次函數﹔即可表示成y= ax2+bx+c(其中a , b , c為常數且a≠0)型式的函數。例如
:y= x2, , y= πx2,, y=100 – 4.9x2, …..等都是二次函數。3.
二次函數的圖形--拋物線重點整理
:描繪
y= x2, , y= 2x2, , y=1/2 x2, ,… y= ax2,,a>0的圖形,並發現這些圖形都是以原點為頂點,y軸為對稱軸,開口向上的對稱圖形。當a的值越大,圖形的開口越小。a的值越小,圖形的開口越大。描繪
y=–x2, , y= –2x2, , y=–1/2 x2, ,… y=bx2,,b<0的圖形,並發現這些圖形都是以原點為頂點,y軸為對稱軸,開口向下的對稱圖形。當b的值越大,圖形的開口越小。a的絕對值越小,圖形的開口越大。描繪
y= x2, +1,y= x2, +2,……y= x2, +k,k>0的圖形,並發現把y= x2, 的圖形向上移動k個單位長,就可以得到y= x2, +k的圖形。描繪
y= x2, -1,y= x2, -2,……y= x2, -k,k>0的圖形,並發現把y= x2, 的圖形向下移動k個單位長,就可以得到y= x2, -k的圖形。
深入探討
1.二次函數通過(0,3) ,(1,4),且對稱於y軸,求此二次函數。
2.設二次函數y= - x2, +4的圖形與x軸相交於A,B兩點,則
(1)![]() =?(2)
=?(2)
![]() 的中點坐標為何?
的中點坐標為何?
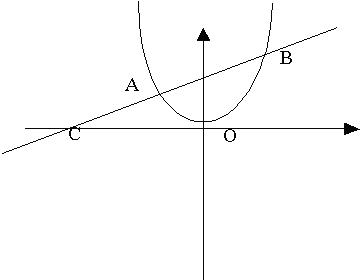
3.如圖,拋物線與直線L交於A(-2,3),C兩點,且直線L交x軸於B(4,0),則C點的坐標為何?

4.拋物線y=1/2 x2,上有相異兩點A.B,設A點之橫坐標為 –2,B為第一象限內之點,若通過A,B之直線L與x軸交於C,且點A為BC之中點,求B點之坐標。
5.如圖,拋物線y= x2,,ABCD為期內接梯形,![]() X軸,E(0,1),梯形的高為3,求梯形ABCD面積
X軸,E(0,1),梯形的高為3,求梯形ABCD面積

2
配方法與二次函數的圖形前言﹕在第一節中,我們發現所有二次函數的圖形都是以
y軸為對稱軸,崎頂點也都是在y軸上,那麼二次函數若不以y軸為對稱圖形,又是如何呢?函數
y=a(x-h)2 之圖形,可由y= ax2,之圖形向左或向右平移h單位而得。y= ax2,
向右平移h單位長,就得到y=a(x-h)2 ,頂點在(h,0)。y= ax2,
向左平移h單位長,就得到y=a(x+h)2 ,頂點在(-h,0)。函數
y=a(x-h)2 +k之圖形可由y= ax2,之圖形向左或向右平移h單位,再向上或向下平移k單位而得。
重點整理 二次函數y= ax2,+bx+c圖形與兩軸的關係
二次函數圖形與y軸必有一交點,其焦點坐標﹕
令x=0代入二次函數,得y之值為c,即可求出與y軸之焦點坐標為(0,c)。
二次函數的圖形與x軸之相交情形﹕
令y=0,解方程式 ax2,+bx+c=0,再由判別式(b2-4ac)可得知。
有關圖形的其他討論如下表﹕
| 判別式(b2-4ac) | b2-4ac>0 | b2-4ac=0 | b2-4ac<0 |
| 此函數所決定之 方程式根之性質 |
兩相等的根 | 無解 | |
| 拋物線與x軸之交點 | 相異兩交點 | 一交點(相交) | 無交點 |
|
a>0( 開口向上) |
 |
 |
 |
|
a<0( 開口向下) |
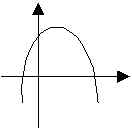 |
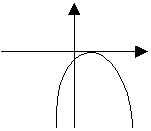 |
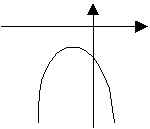 |
深入探討
1.已知二次函數y= -x2+4x-3,寫出下列各點的坐標﹕
頂點
圖形與y軸的交點
圖形與x軸的交點
2.二次函數y= x2-4x-5的圖形與x軸交於A,B兩點,與Y軸相交於C點,頂點為D點,求﹕
中點坐標
C
點坐標D
點到x軸的距離Δ
ABD的面積
3.設二次函數y=kx2-4x+(k-3)與x軸只相交於一點,求(1)k值。(2)交點坐標。
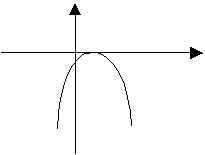
4.若二次函數y= ax2+bx+c的圖形如右圖所示,試判別a . b . c . b2-4的正負關係。
1-3
二次函數的最大值與最小值
重點整理
利用二次函數圖形的頂點位置以及開口方向,求得此二次函數的最大值或最小值。
2.
二次函數y= ax2+bx+c(a當
a> 0時,y=a(x-h)2 +k當
a< 0時,y=a(x-h)2 +k
3.
利用二次函數本身而不惜借助於它的圖形,討論初它的最大值或最小值。a> 0時,則當x= -當
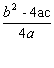 為最小值。
為最小值。
當
a< 0時,則當x= -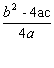 為最大值。
為最大值。
利用二次函數解決一些有關最大值或最小值簡單的應用問題。
深入探討
1.(1) y=x2-6x+10且1![]() x
x![]() 4,求最大值及最小值。
4,求最大值及最小值。
(2) y=x2-4x+3且-5![]() x
x![]() 1,求最大值及最小值。
1,求最大值及最小值。
2.
y=2x2-bx+58有最小值8,求b值
二次函數y=-2x2+ax+b且x=1時,y有最大值為3,求a . b之值。
3.對於二次函數y=ax2+bx+c。
若其圖形通過(0,8),(1,5),(2,6)三點,求此二次函數。
承題(1)將此二次函數配方成y=p(x+q)2+r,求p+q+r。
承題(2),若-1
x
1,室求此二次函數之最小值。
4.請將30分成兩數,使其乘積為最大。
5.把20公分長線段分成兩段,以此兩段為編,做兩正方形,求面積和的最小值。