；如果你把一個扁平的三角形上、下加厚，就可以得到一個三角柱，如圖：
，像科學家牛頓用來把光分成彩虹光譜的稜鏡形狀，像我們小學自然課中教我們用三面鏡子做成的萬花筒;如果同學們把四個三角形搭在一個正方形上方，便成了金字塔！由幾個三角形或是多邊形便可以形成了佔有三度空間的立體圖形。本章就是要告訴同學生活中的平面圖形、立體圖形，在這裡除了課本基本的介紹外，我們再深入淺出的給同學介紹整理一些理念、筒整一些概念，祈使同學在幾何圖形中的學習更加完善。第
2章 簡單的幾何圖形
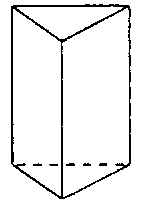
幾何試探究「空間」各種性質的一門學科。從最簡單的一個點，兩個點連成線，三個點連成線形成了面。由點、線、面構成了浩瀚的幾何世界。同學們可曾注意到，許多詞、許多事都和「三」沾上了關係，沾上了邊？例如：「三」隻小豬的故事、「三」劍客、「三」個臭皮匠勝過一個諸葛亮、生日許「三」個願、「三」振出局、「三」輪車．．．．．．。當然啦！這裡我們要說的是我們幾何圖形中最基本也是最簡單的「三角形」，它有三個邊、三個角。三角形是個「平面」圖形，它們只佔有平面的二度空間。但是，如果你把四個三角形接合成一個封閉的形狀，便會做出一個四面體，如圖： ；如果你把一個扁平的三角形上、下加厚，就可以得到一個三角柱，如圖： ，像科學家牛頓用來把光分成彩虹光譜的稜鏡形狀，像我們小學自然課中教我們用三面鏡子做成的萬花筒;如果同學們把四個三角形搭在一個正方形上方，便成了金字塔！由幾個三角形或是多邊形便可以形成了佔有三度空間的立體圖形。本章就是要告訴同學生活中的平面圖形、立體圖形，在這裡除了課本基本的介紹外，我們再深入淺出的給同學介紹整理一些理念、筒整一些概念，祈使同學在幾何圖形中的學習更加完善。
正多面體：
如果一個多面體的每個面都是全等的正多邊形，而且過每個頂點都有同樣多個面拼在一起，這個多面體就是正多面體。
種類：
在一個多面體中，過每個頂點都有同樣多個面拼在一起，到底過每個頂點「至少」要有多少個面乒在一起呢？同學們應不難發現，一個面或兩個面都不行，組合起來都不是並的形狀，至少得有三個面才可以。
現在我們來想想正多面體有幾種？我們已經知道至少三個面，而每個面也都市政多邊形，根據這些的討論如下：
《1》用正三角形
來拼
（i）每個頂點三個面
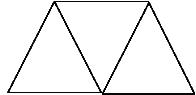
→也就是每個頂點用三個正三角形來拼。這時候拼出來的是正四面體，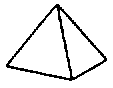
它的展開圖是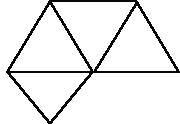
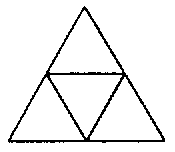
（ii）每個頂點四個面
→也就是每個頂點用四個正三角形來拼。這時候拼出來的是正八面體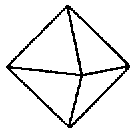
，
它的展開圖是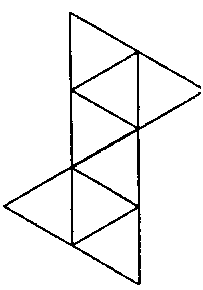
（iii）每個頂點五個面︰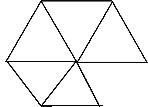
→也就是每個頂點用五個正三角形來拼。這時候拼出來的是正二十面體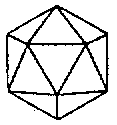
，
它的展開圖是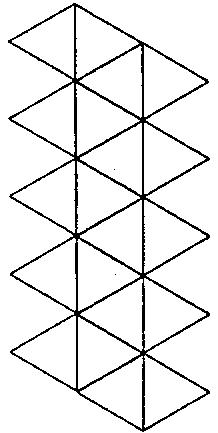
（iv）每個頂點六個面︰
→也就是每個頂點用六個正三角形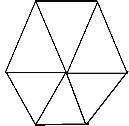
來拼.但是我們是拼不出來的，
因為正三角形的每個內角都是60°，六個角的合是360°，也就是六個正三角形拼出來的已經是平面圖形，所以不可能拼出正多面體。
（v）每個頂角只要比六個面多，各角的合也必定大於360°，所以也都不可能拼出正多面 體,
由以上五點的討論，我們知道，如果要拼出正多面體時，每個頂點用正三角形來拼時，只有三種正多面體,
《2》用正方形來拼︰
（i）每個頂點三個面︰
→也就是每個頂點用三個正方形
來拼，這時候拼出來的是正六面體，
也就是正方體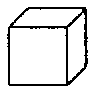
，它的展開圖是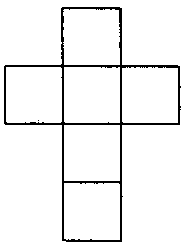
（ii）每個頂點四個面︰
→也就是每個頂點用四個正方形
來拼，但是是拼不出來的，因為正方形的每個內角都是90°，四個角的合是360°，如同正三角形來拼圖的討論，我們同樣可以知道每個頂點用四個面以上時，都不可能拼出正多面體。
由以上兩點的討論，我們知道，如果要拼出正多面體時，每個頂點用正方形來拼時，只有一種多面體,
《3》用正五邊形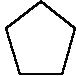
來拼︰
（i） （i）每個頂點三個面︰
→也就是每個頂點用三個正五邊形
來拼，這時候拼出來的是正十二面體
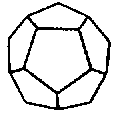,它的展開圖是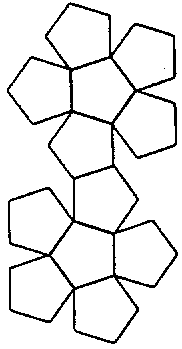
（ii）每個頂點四個面，但是拼不出來，因為正五邊形的每個內角是108°，四個內角合超過360°，仿前面的討論我們知道每個頂點用四個面以上時，都不可能拼出正多面體
由以上兩點的討論，我們知道如果要拼出正多面體時，每個頂點用正五邊形來拼時只有一種正多面體
《4》用正六邊形來拼︰
（i）每個頂點三個面︰
→也就是每個頂點用三個正六邊形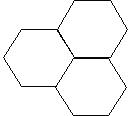
來拼，但是拼不出來的，因為正六邊的每個內角都是360°，如同正三角形來拼圖的討論,我們同樣可以知道每個頂點用三個面以上時，都不可能拼出正多面體
由以上討論可知，用正六邊形，或邊數更多的正多邊形來拼是不可以的，因為三個角的和都超過360°，不可能再拼出正多面體。.
綜合以上（1）到（4）的討論，我們知道正多面體共有五種,就是正四面體、正六面體、正八面體、正十二面體和正二十面體，這個事實通常被稱為正多面體定理.。
現在我們計算各種正多面體頂點數和邊數。以正十二面體為例來說明︰
因為正十二面體的每個面都是正五邊形，它的面有5個頂點，12個面,一共有5 ×12 ﹦60個頂點，但是從每一個頂點看過去，它都是用三個正五邊形來拼成的，因此每一個頂點都被算了三次，所以正十二邊形共有60 ÷3﹦20個頂點；再來看邊的情形，每個面有5個邊，12個面共有5 ×12﹦60邊，但是每個邊都是由兩個面共用，,其實都被算了兩次，所以正十二面體共有60÷2﹦30邊.
n |
3 | 3 | 3 | 4 | 5 |
| m | 3 | 4 | 5 | 3 | 3 |
| 面數 | 4 | 8 | 20 | 6 | 12 |
| 頂點數 | 4 | 6 | 12 | 8 | 20 |
| 邊數 | 6 | 12 | 30 | 12 | 30 |
圖形 |
|
|
|
|
|
| 展開圖 |
|
|
|
|
|
尤拉公式
我們在課本中所介紹的正方體、正方體、角柱、角椎等，都是多面體，現在我們來探討多面體的頂點數、邊數和面數之間的關係，習慣上我們用v(vertex)代表頂點數，f(face)代表面數，e(edge)代表邊數。我們將課本中一些例子的有關資料,列在下表中,並任意加上兩個課本沒有出現過的其他多面體︰
| 種類 | 圖形 | v | f | e |
| 長方體 |
 |
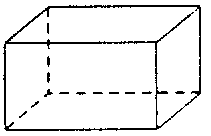8 | 6 | 12 |
| 三角柱 |
|
6 | 5 | 9 |
| 五角柱 |
 |
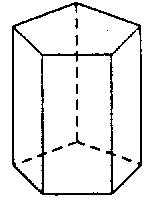10 | 7 | 15 |
| 六角錐 |
 |
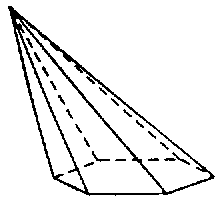7 | 7 | 12 |
| 四角錐 |
 |
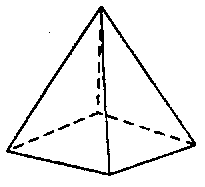5 | 5 | 8 |
| 六面體 |
 |
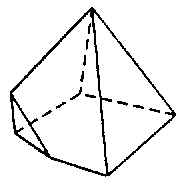7 | 6 | 11 |
| 角錐臺 |
 |
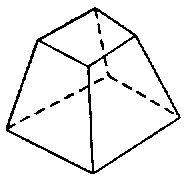8 | 6 | 12 |
在上表中可以看出來 v ﹢f ﹦e ﹢2 或寫成 v － e ﹢f ﹦2
這就是著名的尤拉公式。
在正多面體的討論中,我們用拼圖直觀及簡易內角和的方法來探討正多面體定理，現在我們可以用尤拉公式來作較正式的討論。
像前面討論的一樣，如果一個正多面體的每一面都是正n邊形，而且在每一個頂點的地方都是由m個面拼在一起，我們來頂點數v、邊數e和面數f的值有何限制。
我們先考慮頂點數，因為有f個面，每個面都有n個頂點，所以共有nf個項點，但是每個頂點的地方都是由m個面拼在一起，所以每個頂點都被計算了m次，實際的頂點數是
v ﹦nf ÷m…………………………………………(a)
再來計算邊數，因為有f個面，每個面都有n個邊，所以共有nf個邊，但是每個邊都由相鄰的兩個邊共用，所以每個邊都被計算了兩次，實際的邊數是
e ﹦nd ÷2……………………………………………(b)
把這兩式帶入公式
v － e ＋ f ﹦2
可得
全式除以 nf 得
mn －2m －2n<0
mn －2m －2n＋4<4
(n－2) (m－2)< 4
但m、n 均為正整數且m≧3 ， n≧3，
我們在下表中列出所有可能的m、n值，並解(a)、 (b)、 (c)三式計算出 v、e 和 f 的值
| n-2 | 1 | 1 | 1 | 2 | 3 |
| m-2 | 1 | 2 | 3 | 1 | 1 |
| n | 3 | 3 | 3 | 4 | 5 |
| m | 3 | 4 | 5 | 3 | 3 |
| v | 4 | 6 | 12 | 8 | 20 |
| e | 6 | 12 | 30 | 12 | 30 |
| f | 4 | 8 | 20 | 6 | 12 |
（1） 遠哲教育基金會︰快樂習三角形
（2） 國立編譯館︰數學教師手冊第四冊